Triangle wave, Square wave, Saw tooth wave and "noise" our wave forms often seen in digital synthesizers from its early days.

    


    

Triangle wave (single tone) (mp3/11kb)
Example of its usage (mp3/15kb)

    
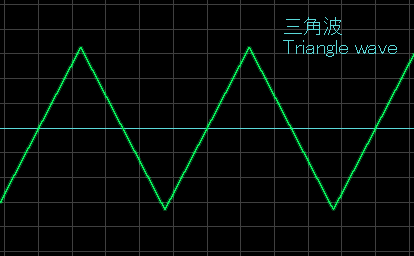
The triangle wave is a simple wave form that comes closest to the smooth tone of a sine wave. This characteristic being more present in the low ends is a major reason sound designers often used this wave form to play base lines in early video game music.

    
The NES system had one triangle wave generator which we will look into later.

    


    


    

Square wave (mp3/13kb)
Example of its usage (mp3/25kb)

    
The square wave is generated when adding up odd harmonics (sine waves with 3,5,7 times the frequency of the basic pitch)

    
The NES system could generate two of these square waves at a time. They were mostly used to play the melody, sound effects and all other cool effects you probably would never have imagined.

    
The above example contains the same phrase played first by a square wave, then by a pulse wave.

    


    


    


    
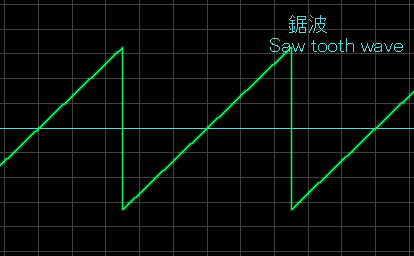
When you add up all harmonics with frequencies multiplied by whole numbers, the waveform of a sine waves gradually becomes closer to the wave form of the "Saw wave" you see above.

    
This waveform is said to be similar to that of a string ensemble. By modifying this wave form, you can easily get a sound similar to a "string" patch stored in most synthesizers.

    
Unfortunatly, the NES system was not able to produce this wave form.

    


    
Noise is basically a "random" wave form When the human ear hears random waves (which is actually the sum of all existing frequencies), the human ear recognizes it as noise. (How hard do you think it is for a computer to spit out a series of random numbers?)


    


    
When you keep on combining sine waves with unrelated frequencies, your wave form will start sounding like noise the more you add. On the other hand, you can reproduce a sine wave out of noise by using a "filter" to exclude all frequencies but the one you desire to leave.


    
The NES system had one noise generator. This was used mainly to simulate snare drums&Hihg-Hat sounds besides sound effects.

    


    


    


    
Since I am no engineer myself, I can only guess that these wave forms were often used in digital synths due to the wave forms simplicity.

    
For example, think of the Saw wave.

    When digitally reproducing a wave form, the algorhythm has to be programmed by someone or another. In case of a saw wave, we can represent the wave form by such methods as,

    

      

        

        Var:Voltage(v =0), Set variables n,m (n>0, m>0)

        Step 1. Increase [v] by [n] steps.

        Step 2. if [v > m] then v = v*(-1)  [v becomes negative]

        Step 3. Return to step 1
 
      
    


    


    
Take the time on the x-axis and voltage on the y-axis. When you repeat the above three steps, you get the graph of a saw wave. (Note that when the amount of [n] increases, you get a steeper line = higher frequency)

    
I know this might be confusing, but I am sure it would have been worse if you tried to draw the smooth curve of a sine wave using basic addition and subtractions.