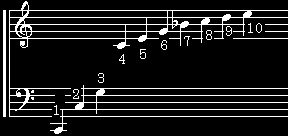ある音Ｎの周波数が２倍、４倍、８倍と、２の累乗倍される度に、音程が１オクターブずつ上がる事は、先の項でも述べました。では、その間の３、５、６、７倍した場合、どのような音程が得られるのでしょう？

    


    これも、ここでは結果だけ記します。

    
元の音を「ド」とすると、１オクターブ上の「ソ」が３倍、２オクターブ上の「ミ」が５倍の周波数を持ちます。それ以降については、以下の図を参考にして下さい。

    この表にあるような、ある音程Ｎの整数倍の周波数を持つ音程を、Ｎの「倍音」と呼びます。

    


    
↑ヘ音記号下の「ド」を基音とする倍音列

    
さて、自然界に存在する音は、必ずと言ってよいほど倍音を含んでおり、この含まれる「倍音の違い」が、そのまま「音色の違い」に反映されます。

    例えば、同じ音程を演奏しても、バイオリンとクラリネットでは明らかに音色が違うでしょう。これは、バイオリンが各倍音を比較的均等に含んでいるのに対し、クラリネットは元となる「基音」の偶数倍（２、４、８...）の周波数を持つ倍音をあまり含んでいないからです。

    
既にお気付きの方もいるかも知れませんが、倍音列で比較的番号の若いものは、セブンスコードの構成音でもあります。上の図でも、「ド」に対する最初の方の倍音は、それぞれ「ド・ソ・ド・ミ・ソ・シ♭」でした。

    この辺りの倍音が豊富なグランドピアノでは、低い方の鍵盤を強く弾いた時に、これらの音程を独立して聞きとることもできます。

    逆に、ドラムやトライアングルなどの打楽器の音程が聞き取りづらいのは、これらがコードの構成音でない「非整数倍音」を多く含んでいるからです。